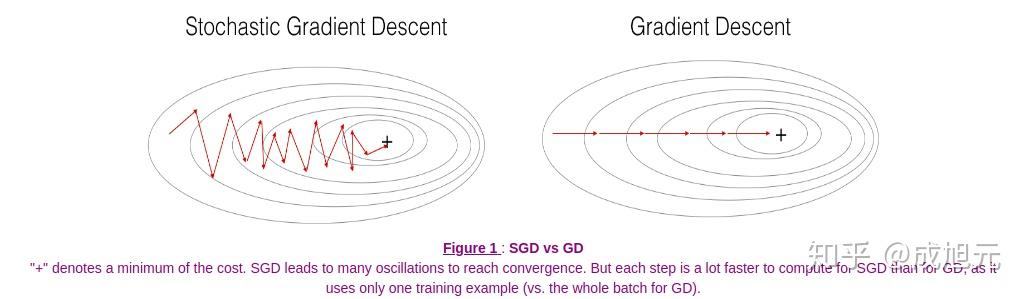
在传统的梯度下降优化Cost的过程中,如果训练数据集非常大(百万以上级别),那么每次在整个数据集上进行多个矩阵运算才能获得一次梯度,因此会导致学习的速率非常缓慢。
因此使用这样一种方法,将m大小的整个数据集划分成多个大小为t的子集,在一个训练轮次(epoch)中,依次使用这些子集来进行梯度下降,这样每个epoch就可以获得 个梯度并进行下降,从而加快了学习速度,这就是Mini Batch 梯度下降方法。
在使用Mini Batch时,除了对数据集和labels进行划分之外,其他任何过程(FP,BP,Cost计算等)都不需要变化,因为W和b的维度都不依赖与数据集大小m,所以在每次使用Mini Batch的时候,相当于使用了一个不同的,较小的数据来进行训练,而通常每个batch的特征分布都是与整个数据集类似的,因此可以达到与整个数据集训练近似的优化效果。
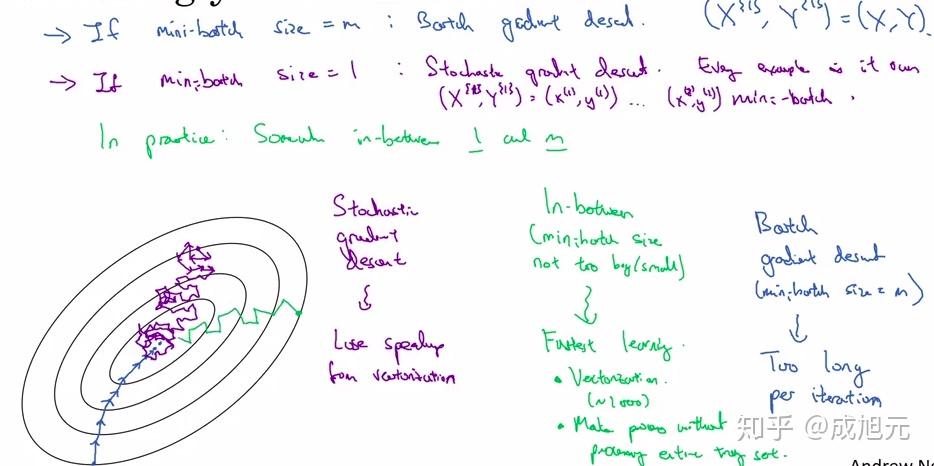
根据Mini Batch Size的大小,可以讲梯度下降分为以下几类:
- Size=m。这就是传统的梯度下降方法,即Batch Gradient Descent,用整个数据集求出一次梯度。这种方法的优点是Cost的值就代表了整个数据集特征,每次梯度下降能保证使Cost减小,因此步长也较大。
- Size=1。这种方法叫做随机梯度下降,每次只使用一个样例来求得一次梯度,这一方法的优点是学习速度很快,对于大型数据集,一个epoch就可以获得成千上完个梯度。但是这种方法由于每个样例的分布差异,噪声很大,Cost的下降不是严格的单调减函数,且靠近最优化点的时候总是在徘徊(没有办法准确到达最优化点,虽然这可以用较小的学习率来解决),如下图。且由于每次计算单个样例,无法使用向量化来加速计算。
- 1<Size<m。即Mini Batch Gradient Descent。综合了上述两种情形的优点。Batch Size也作为一个可以调整的超参数。
在开率是否要使用Mini Batch的时候,一般遵循以下几种原则:
- 如果数据集非常小(如m<2000),直接使用Batch Gradient Descent。
- 如果数据集较大,一般选择64、128、256、512等2的整数次幂作为Mini Batch Size(这与内存的Align实现有关)。
- 保证Mini Batch Size小于内存或者显存。
- 在使用Mini Batch时,每一个epoch都要将整个数据集和对应的labels进行一次shuffle,以保证随机性,不会对batch的顺序发生过拟合。
在拟合一组含有噪声但是有明显分布点的分布趋势时,可以用到指数加权平均这一方法,即每在第n次计算当前值时,都将前n-1的值通过加权的方式求和,使计算当前值能够保存前面的数据分布趋势,而又由于加权衰减,是更早的数据影响的更小,比直接用平均值的方式更优。
其中 分别为当前的估计值和当前的数据点。
通过推导,可知 约为前
个数据点的平均值,因为有这样一个结论,对于小数
,有
又因为,把 展开,可以发现它的值实际上就是由一个指数衰减函数和数据点做内积的结果,而当这个指数衰减到
以下就可以近似忽略内积的值了,因此取到t一直到往前
个数据点的平均值就是
的近似了。将
换成
,就得到了上述结论。
在使用指数加权平均时,还有一点需要注意,就是在t接近0,即数据点的开始部分,由于 ,会导致前几个数据非常小(接近0,可以展开前几个式子进行推导得出),因此要加入bias修正项,即
这样在t较小的时候,分子较大,可以将估计值拉高,而t较大的时候, 接近于1,对拟合结果基本没有影响,就可以忽略了。
指数加权平均的作用就是可以通过调节 参数来调整当前
保存了前多少个t的信息。
当我们使用Mini Batch而是Batch梯度下降时,由于一次梯度下降的计算是由一部分数据样本获得的,因此在Cost平面中,这一次梯度下降移动的方向不一定是朝着全局最优点前进的,而是有一定偏差,这些偏差的结果就是梯度下降的路线有很多噪声和振荡,导致学习速度降低。
动量梯度下降就是为了解决振荡导致学习速度降低的问题。引入物理学中动量的概念,每一次梯度下降的方向和距离都受到之前梯度下降的方向和速度的影响,如下图所示,使用普通的梯度下降,每次下降的方向只与当前点计算的导数有关,存在振荡;而引入动量之后,W方向的分量由于一直是右移,因此积累的动量方向也是一直向右,从而使优化路线更快的走向右侧的最优点,而b方向的分量由于一直上下振荡,因此累积的动量基互相抵消,使优化路线更少的向b方向移动,结合在一起就能够提高学习速度。
一个直观感受是,寻找最优值的过程是小球滚到山底的过程,传统的梯度下降没有速度,即给小球一个推力,小球下降一段距离(梯度大小)就停止了,没有惯性,梯度是什么方向小球就往什么方向滚动;而动量梯度下降是小球在下降的过程中不断积累速度,每次算出的梯度是给小球往梯度方向碰了一下(加了一个冲量),最终小球的运行方向是有他以前积累的速度和冲量方向合成得到的。

在应用动量梯度下降时,用以下的方法更新参数:
其中 就是对应的参数(W,b等)
RMS prop是从学习率的角度解决振荡和加快学习速度的,实际上是对AdaGrad和AdaDelta的改进(这两个算法在这里不多加描述,基本思路是对于每个参数W或b,自动的适配其对应的学习率,而不是使用全局统一的学习率)。
RMS prop的思路是,如果某个参数方向的摆动幅度大(噪音或振荡大),那么就说明这一参数的方差大,那么如果动态的将该参数方向的学习率降低,就能够减小梯度下降步长,从而减小摆动幅度,反之增加步长,使其能够更快的到达最优点。因此在RMS Prop中,用梯度除以该参数的指数加权平均方差来实现这一功能。
在应用RMS prop时,用以下的方法更新参数:
其中 是为了防止分母为0增加的补偿项,一般取值
。
Adam方法结合了动量和RMS prop方法的优点,目前业界已经证明Adam适用于很多架构的网络,应用较为广泛。
由于上文已经解释了动量和RMS prop的工作原理,因此这里直接写出Adam方法的计算过程:
这里要注意,用于更新权值的 值均是经过初始值修正的值。
在实现过程中,对于 的值,一般选取
。
在训练的过程中,如果始终使用相同的学习率,则在接近优化目标时,很可能由于步长过大而导致一次又一次的错过目标,最终在最优值附近摆动,因此采用学习率衰减这一技术,是学习率在训练过沉程中随着训练次数的增加而衰减。
实现学习率衰减有若干方式,如
其中decay_rate是学习率衰减,epoch是整个数据集的训练轮次。
或者指数衰减
或者
另外还可以使用离散形式的 。
局部最优值的出现是因为人们对于2维Cost平面的直观想象而误导的结果,如图,在2维的Cost平面上,确实很容易出现局部最优的情况,因为只需要出现w1和w2均为函数的谷底就会导致出现一个局部极小值。
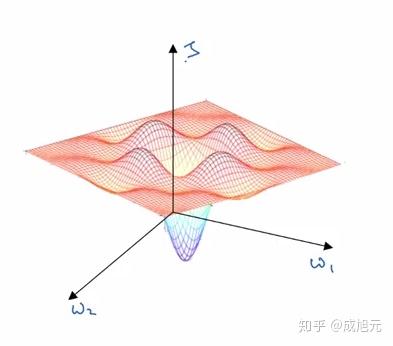
但是在实际的神经网络中,存在着几万甚至几十上百万的参数,他们张成的空间如果想要出现局部极小值,则要几万个参数在同一点全部是谷底形状,而这样的概率太小。
实际上,在多维度参数优化时,更可能出现的的是鞍点,如下图,即某些参数是分布是谷底形状,而某些参数分布是峰顶形状。
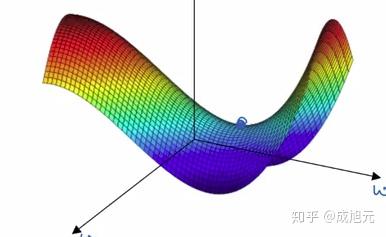
在鞍点处的梯度也是处处为0,但是如果使用SGD或者Mini Batch,每一次的梯度计算都有一定的随机性,很容易就会从鞍点滑下来,并继续优化过程。